Методы изучения фигуры земли

Содержание

	Предисловие	3
	Времена года, некоторые постоянные	5
	Звездное время	6
	Эфемерида Солнца	10
	Прямоугольные экваториальные координаты Солнца	26
	Аберрация, параллакс, средняя долгота Солнца, наклон эклиптики, нутация наклона	34
	Средняя долгота Луны, положение ее средней орбиты и среднего экватора	35
	Эфемерида Луны	36
	Прямое восхождение, склонение и геоцентрическое расстояние Луны	52
	Коэффициенты полиномов Чебышева, Луна	60
	Фазы Луны, перигей и апогей	60
	Гелиоцентрические координаты планет	61
	Оскулирующие элементы внутренних планет	66
	Оскулирующие элементы внешних планет	67
	Эфемерида Меркурия	68
	Эфемерида Венеры	76
	Эфемерида Марса	84
	Эфемерида Юпитера	92
	Эфемерида Сатурна	100
	Эфемерида Урана	108
	Эфемерида Нептуна	116
	Эфемерида Плутона	124
	Положение и скорость Земли	126
	Прецессия и нутация	127
	Редукционные величины на 0h земного времени	142
		150
	Планетные конфигурации	162
	Эфемерида для физических наблюдений Солнца	166
	Эфемерида для физических наблюдений Луны	170
	Эфемерида для физических наблюдений Меркурия	178
	Эфемерида для физических наблюдений Венеры	186
	Эфемерида для физических наблюдений Марса	190
	Эфемерида для физических наблюдений Юпитера	198
	Физические характеристики Солнца, Луны и больших планет	205
	Элементы вращения планет	205
	Эфемерида для физических наблюдений Сатурна	206
	Кольца Сатурна	212
	Эфемерида для физических наблюдений Урана	214
	Эфемерида для физических наблюдений Нептуна	216
	Восходы и заходы Солнца для широт от +30° до +70°	218
	Восходы и заходы Луны для широт от +30° до +70°	226
	Сокращенные обозначения созвездий	258
	Сокращенные обозначения каталогов	258
	Средние места звезд (J2020.5)	259
	Средние места близполюсных звезд (J2020.5)	273
	Средние места звезд (ICRS)	274
	Средние места близполюсных звезд (ICRS)	288
	Редукционные величины на 0h звездного динамического времени	289
	Второй порядок редукционных величин	297
	Видимые места звезд	301
	Видимые места близполюсных звезд	484
	Таблицы для определения широты по наблюдениям Полярной	578
	Таблица высот и азимутов Полярной	583
	Угол вращения Земли и уравнение начал	586
	Небесная промежуточная система CIRS	590
	Матрица перевода в систему CIO	594
	Вспомогательные таблицы
I.	Юлианский период	603
IIa.	Перевод среднего времени в звездное (с точностью до 0.01s)	608
IIb.	Перевод звездного времени в среднее (с точностью до 0.01s)	609
IIIa.	Перевод среднего времени в звездное (с точностью до 0.001s и 0.0001s)	610
IIIb.	Перевод звездного времени в среднее (с точностью до 0.001s и 0.0001s)	611
IVa.	Обращение минут и секунд в доли градуса и обратно	612
IVb.	Обращение десятичных долей градуса в минуты и секунды	613
V.	Выражение дуги во времени	614
VI.	Обращение минут и секунд в доли часа	614
VII.	Обращение часов, минут и секунд в доли суток	615
VIIIa.	Элементы земного сфероида ПЗ-90. Вычисление геоцентрических координат точек земной поверхности	616
VIIIb.	Элементы земного сфероида МГГС. Вычисление геоцентрических координат точек земной поверхности	617
IX.	Коэффициенты интерполяционной формулы Бесселя	618
X.	Рефракция (точность 1″ )	619
XI.	Рефракция (точность 0.1″)	620
	Объяснение к Астрономическому ежегоднику на 2020 год
1.	Общие замечания	621
2.	Интерполирование	630
3.	Звездное время	633
4.	Переход от одной системы счета времени к другой	634
5.	Фундаментальные эфемериды Солнца, Луны и больших планет	638
6.	Эфемерида Солнца: экваториальные и эклиптические координаты	640
7.	Прямоугольные экваториальные координаты Солнца	644
8.	Средние элементы орбиты Солнца. Средние элементы лунной орбиты и экватора	645
9.	Эфемерида Луны. Коэффициенты полиномов Чебышева. Фазы Луны, перигей, апогей	645
10.	Гелиоцентрические координаты планет. Оскулирующие элементы	647
11.	Эфемериды больших планет	648
12.	Положение и скорость Земли. Прецессия и нутация	650
13.	Редукционные величины	652
14.	Затмения	653
15.	Планетные конфигурации и другие астрономические явления	657
16.	Эфемерида для физических наблюдений Солнца	657
17.	Эфемерида для физических наблюдений Луны	658
18.	Планетоцентрические и планетографические координаты Земли и Солнца	659
19.	Эфемериды для физических наблюдений планет	661
20.	Кольца Сатурна	662
21.	Восходы и заходы Солнца и Луны	663
22.	Средние места звезд	664
23.	Видимые места звезд	666
24.	Видимые места близполюсных звезд	674
25.	Таблицы для определения широты по наблюдениям Полярной	677
26.	Угол вращения Земли и уравнение начал	678
27.	Параметры небесной промежуточной системы	679
28.	Матрица преобразования от ICRS к CIRS	679
29.	Приложение к Астрономическому ежегодннику на 2020 год	681
	Предметный указатель	682

Покрытия звезд Луной, видимые в городах России

В таблице приведены: момент геоцентрического соединения Луны и звезды по
всемирному времени, номер звезды по каталогу AE, номер звезды по
каталогу HIPPARCOS, название звезды, названия пунктов наблюдения.

Все вычисления выполнены в рамках программного комплекса ЭРА на основе
теории движения больших планет и Луны EPM.

	d	h	AE	HIP	Назв.
Дек.	31	10	700	112716	τ Aqr	Казань Москва Екатеринбург Зеленчукская Томск
Янв.	07	17	114	20648	68 δ3 Tau5	Пулково
Янв.	09	00	158	26451	ζ Tau	Томск
Янв.	09	15	176	29655	η Gem	Владивосток Томск Зеленчукская Екатеринбург
Янв.	09	18	181	30343	μ Gem	Москва Екатеринбург Пулково Казань Зеленчукская Владивосток Томск
Февр.	05	10	158	26451	ζ Tau	Томск Екатеринбург Казань
Февр.	07	03	205	35550	δ Gem	Пулково
Март	02	12	116	20889	ε Tau	Владивосток
Март	04	11	176	29655	η Gem	Москва Томск Казань Екатеринбург Пулково Зеленчукская
Март	04	14	181	30343	μ Gem	Москва Пулково Екатеринбург Казань
Март	29	19	116	20889	ε Tau	Москва Зеленчукская Казань Екатеринбург Пулково
Март	31	18	176	29655	η Gem	Томск
Март	31	22	181	30343	μ Gem	Казань
Апр.	22	11	39	7884	ν Psc	Зеленчукская
Апр.	26	00	116	20889	ε Tau	Владивосток
Май	15	19	700	112716	τ Aqr	Владивосток
Май	23	06	116	20889	ε Tau	Казань Москва Пулково Зеленчукская Томск Екатеринбург
Июнь	12	03	700	112716	τ Aqr	Зеленчукская Пулково Екатеринбург Москва Казань Томск
Июнь	19	14	116	20889	ε Tau	Пулково Казань Москва
Июль	16	22	116	20889	ε Tau	Екатеринбург Владивосток Казань Томск
Авг.	05	20	700	112716	τ Aqr	Томск Екатеринбург Казань Зеленчукская Москва
Авг.	13	23	136	23497	ι Tau	Владивосток
Авг.	23	17	342	69427	κ Vir	Пулково
Авг.	25	18	389	78820	β Sco	Пулково
Сент.	06	00	39	7884	ν Psc	Казань Москва Томск Екатеринбург Зеленчукская
Сент.	10	07	136	23497	ι Tau	Казань Томск Екатеринбург Москва Пулково Зеленчукская
Сент.	24	11	451	90496	λ Sgr	Владивосток Томск
Окт.	07	14	136	23497	ι Tau	Владивосток
Окт.	17	12	342	69427	κ Vir	Пулково Москва Зеленчукская Екатеринбург Казань
Окт.	19	10	389	78820	β Sco	Пулково Зеленчукская Москва
Окт.	26	15	700	112716	τ Aqr	Екатеринбург Казань Томск Москва Зеленчукская
Окт.	30	13	39	7884	ν Psc	Владивосток
Нояб.	03	20	136	23497	ι Tau	Москва Пулково
Нояб.	18	03	451	90496	λ Sgr	Владивосток
Нояб.	26	19	39	7884	ν Psc	Томск Пулково Зеленчукская Екатеринбург Москва Казань
Дек.	11	09	342	69427	κ Vir	Пулково Казань Зеленчукская Москва
Дек.	28	09	136	23497	ι Tau	Томск

ЭЛЛИПС

ЭЛЛИПС — множество точек плоскости , для каждой из которых
сумма расстояний до двух данных точек  и , лежащих в , есть величина постоянная, большая, чем
расстояние между  и , и равная данному
числу  (или
отрезку ).
Точки  и  называются фокусами Э. Расстояние между фокусами,
обозначаемое через ,
называется фокальным. Данное число (отрезок)  называется большой осью.

Э. можно начертить так. Взяв
нерастяжимую нить длиной , закрепим ее концы в точках  и  (рис. 142).
Зачтем, натянув эту нить острием карандаша, будем двигать острие карандаша по
бумаге. Траектория движения острия карандаша и опишет замкнутую кривую — Э.,
для которой , отрезки  и  называются
фокальными радиусами.

Рис. 142

Каноническое (простейшее) уравнение Э. в
прямоугольных декартовых координатах имеет вид:

,

где
. Число
(отрезок)  называется
малой осью Э.

Из уравнения Э. вытекает, что , . Отсюда следует, что координаты
точек эллипса удовлетворяют условиям: , , т. е. Э. расположен внутри
прямоугольника со сторонами  и . Из уравнения Э. также следует, что Э. имеет
центр и две оси симметрии.

Число  называется эксцентриситетом
Э. Для Э. всегда .
Если  (фокусы
совпадают), то Э. вырождается в окружность, для которой совпадающие фокусы
являются центром, а эксцентриситет  (так как при этом ).

Параметрические уравнения Э. имеют вид:

, ,

Они
легко усматриваются из рисунка 143: если отрезок постоянной длины скользит
своими концами по двум взаимно перпендикулярным прямым, то точка  этого отрезка опишет Э.
Если точку  взять
на продолжении отрезка  (на рисунке точка ), то описываемая ею кривая будет
также Э. На указанном свойстве построен эллиптический циркуль — прибор,
вычерчивающий Э. с различными осями.

Рис. 143

Если спроектировать какую-либо
окружность на плоскость, не перпендикулярную и не параллельную плоскости
окружности, то в проекции получится Э. Если круговой цилиндр пересечь наклонной
плоскостью или круговой конус пересечь наклонной плоскостью, имеющей различные
общие точки с противоположными образующими конуса, то в сечении получится Э.

Прямые, уравнения которых  называются директрисами Э.

Касательная  к Э. составляет равные углы с
фокальными радиусами, проведенными в точку касания (рис. 144). Отсюда
вытекает, что перпендикуляр  к касательной в точке касания составляет
равные углы с фокальными радиусами. Это свойство можно истолковать как свойства
углов падения и отражения, изучаемых в оптике: если точечный источник света
поместить в фокусе  и луч света
направить на зеркальную поверхность  по , то отраженный луч пойдет по , т. е. попадет в
точку . Отсюда
происходит и название фокуса (от лат. focus — очаг, огонь).

Рис. 144

Свойства Э. используются в технике в
конструкциях некоторых станков, где имеются зубчатые шестерни эллиптической
формы. Траектории движения планет нашей солнечной системы являются различными
Э. Свойства Э. используются также при изучении законов движения планет —
законов Кеплера, Полярное уравнение Э. имеет вид:

,

где
,  — фокальный параметр.

При вращении Э. вокруг одной из его осей
получается поверхность 2-го порядка — эллипсоид вращения. См. Конические
сечения.

Греч.  — недостаток, в смысле недостатка
эксцентриситета до 1. Для Э. .

ОСНОВНЫЕ ЛИНИИ И ПЛОСКОСТИ ЗЕМНОГО ЭЛЛИПСОИДА

При определении положения точек на поверхности Земли и на поверхности земного эллипсоида пользуются некоторыми линиями и плоскостями.
Известно, что точки пересечения оси вращения земного эллипсоида с его поверхностью являются полюсами, один из которых называется Северным Рс, а другой – Южным Рю (рис. 2.4).

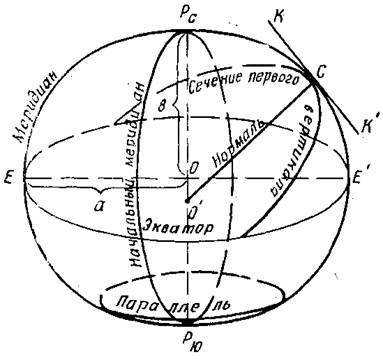
Рис. 2.4. Основные линии и плоскости земного эллипсоида

Сечения земного эллипсоида плоскостями, перпендикулярными к малой его оси, образуют след в виде окружностей, которые называются параллелями. Параллели имеют различные по величине радиусы. Чем ближе расположены параллели к центру эллипсоида, тем больше их радиусы. Параллель с наибольшим радиусом, равным большой полуоси земного эллипсоида, называется экватором

Плоскость экватора проходит через центр земного эллипсоида и делит его на две равные части: Северное и Южное полушария.
Кривизна поверхности эллипсоида является важной характеристикой. Она характеризуется радиусами кривизны меридианного сечения и сечения первого вертикала, которые называются главными сечениями
Сечения поверхности земного эллипсоида плоскостями, проходящими через его малую ось (ось вращения), образуют след в виде эллипсов, которые называются меридианными сечениями.
На рис. 2.4 прямая СО’, перпендикулярная к касательной плоскости КК’ в точке ее касания С, называется нормалью к поверхности эллипсоида в этой точке

Каждая нормаль к поверхности эллипсоида всегда лежит в плоскости меридиана, а следовательно, пересекает ось вращения эллипсоида. Нормали к точкам, лежащим на одной параллели, пересекают малую ось (ось вращения) в одной и той же точке. Нормали к точкам, расположенным на разных параллелях, пересекаются с осью вращения в различных точках. Нормаль к точке, расположенной на экваторе, лежит в плоскости экватора, а нормаль в точке полюса совпадает с осью вращения эллипсоида.
Плоскость, проходящая через нормаль, называется нормальной плоскостью, а след от сечения этой плоскостью эллипсоида – нормальным сечением. Через любую точку на поверхности эллипсоида можно провести бесчисленное множество нормальных сечений. Меридиан и экватор являются частными случаями нормальных сечений в данной точке эллипсоида.
Нормальная плоскость, перпендикулярная к плоскости меридиана в данной точке С, называется плоскостью первого вертикала, а след, по которой она пересекает поверхность эллипсоида, – сечением первого вертикала (рис. 2.4).
Взаимное положение меридиана и любого нормального сечения, проходящего через точку С (рис. 2.5) на данном меридиане, определяется на поверхности эллипсоида углом А, образованным меридианом данной точки С и нормальным сечением

2.4 прямая СО’, перпендикулярная к касательной плоскости КК’ в точке ее касания С, называется нормалью к поверхности эллипсоида в этой точке. Каждая нормаль к поверхности эллипсоида всегда лежит в плоскости меридиана, а следовательно, пересекает ось вращения эллипсоида. Нормали к точкам, лежащим на одной параллели, пересекают малую ось (ось вращения) в одной и той же точке. Нормали к точкам, расположенным на разных параллелях, пересекаются с осью вращения в различных точках. Нормаль к точке, расположенной на экваторе, лежит в плоскости экватора, а нормаль в точке полюса совпадает с осью вращения эллипсоида.
Плоскость, проходящая через нормаль, называется нормальной плоскостью, а след от сечения этой плоскостью эллипсоида – нормальным сечением. Через любую точку на поверхности эллипсоида можно провести бесчисленное множество нормальных сечений. Меридиан и экватор являются частными случаями нормальных сечений в данной точке эллипсоида.
Нормальная плоскость, перпендикулярная к плоскости меридиана в данной точке С, называется плоскостью первого вертикала, а след, по которой она пересекает поверхность эллипсоида, – сечением первого вертикала (рис. 2.4).
Взаимное положение меридиана и любого нормального сечения, проходящего через точку С (рис. 2.5) на данном меридиане, определяется на поверхности эллипсоида углом А, образованным меридианом данной точки С и нормальным сечением.

Рис. 2.5. Нормальное сечение

Этот угол называется геодезическим азимутом нормального сечения. Он отсчитывается от северного направления меридиана по ходу часовой стрелки от 0 до 360°.
Если принять Землю за шар, то нормаль к любой точке поверхности шара пройдет через центр шара, а любая нормальная плоскость образует на поверхности шара след в виде окружности, которая называется большим кругом.

Референц-эллипсоид

Фигура референц-эллипсоида наилучшим образом подходит для территории отдельной страны или нескольких стран. Как правило, референц-эллипсоиды принимаются для обработки геодезических измерений законодательно. В России/СССР с по 2012 использовалось 3 основных системы координат основанных на (СК-42, СК-63 и СК-95). С 2012 ПП РФ 1463 и 1240 от 28 декабря 2012 года и от 24 ноября 2016 соответственно использование СК-42 и СК-95 допускается до 1 января 2021 года).

— эллипсоиды ГСК-2011 и ПЗ-90.11. Эллипсоиды СК-95 и Красовского выводятся из употребления к 1 января 2021 г. В США общеупотребительным является референц-эллипсоид WGS-84.

Ориентирование референц-эллипсоида в теле Земли подчиняется следующим требованиям:

1. Малая полуось эллипсоида (b) должна быть параллельна оси вращения Земли.
2. Поверхность эллипсоида должна находиться возможно ближе к поверхности геоида в пределах данного региона.

Для закрепления референц-эллипсоида в теле Земли необходимо задать геодезические координаты B, L, H начального пункта геодезической сети и начальный азимут A на соседний пункт. Совокупность этих величин называется исходными геодезическими датами.

Основные референц-эллипсоиды и их параметры

Учёный	Год	Страна	a, м	1/f
	1800	Франция	6 375 653	334,0
	1810	Франция	6 376 985	308,6465
	1819	Финляндия,Российская Империя	6 376 896	302,8
	1830		6 377 563,4	299.324 964 6
	1830	Индия, Пакистан, Непал, Шри-Ланка	6 377 276,345	300.801 7
	1841	Германия, Россия (до 1942 г.)	6 377 397,155	299.152 815 4
Теннер	1844	Россия	6 377 096	302.5
	1866	США, Канада, Лат. и Центр. Америка	6 378 206,4	294.978 698 2
	1880	Франция, ЮАР	6 377 365	289.0
	1880		6 378 249	293.5
	1907		6 378 200	298,3
	1910	Европа, Азия, Ю. Америка, Антарктида	6 378 388	297,0
Хейсканен	1929		6 378 400	298,2
	1936	СССР	6 378 210	298,6
	1942	СССР, советские республики, Восточная Европа, Антарктида	6 378 245	298.3
	1956	Индия, Непал	6 377 301,243	300.801 7
IAG-67	1967		6 378 160	298.247 167
WGS-72	1972		6 378 135	298.26
IAU-76	1976		6 378 140	298.257

Длина дуги эллипса

Длина дуги плоской линии определяется по формуле:

l=∫t1t2(dxdt)2+(dydt)2dt.{\displaystyle l=\int \limits _{t_{1}}^{t_{2}}{\sqrt {\left({\frac {dx}{dt}}\right)^{2}+\left({\frac {dy}{dt}}\right)^{2}}}\,dt.}

Воспользовавшись параметрическим представлением эллипса получаем следующее выражение:

l=∫t1t2a2sin2⁡t+b2cos2⁡tdt.{\displaystyle l=\int \limits _{t_{1}}^{t_{2}}{\sqrt {a^{2}\sin ^{2}t+b^{2}\cos ^{2}t}}\,dt.}

После замены b2=a2(1−e2){\displaystyle b^{2}=a^{2}\left(1-e^{2}\right)} выражение для длины дуги принимает окончательный вид:

l=a∫t1t21−e2cos2⁡tdt,e1.{\displaystyle l=a\int \limits _{t_{1}}^{t_{2}}{\sqrt {1-e^{2}\cos ^{2}t}}\,dt,\;\;\;e

Получившийся интеграл принадлежит семейству эллиптических интегралов, которые в элементарных функциях не выражаются, и сводится к E(t,e){\displaystyle E\left(t,e\right)}. В частности, периметр эллипса равен:

l=4a∫π21−e2cos2⁡tdt=4aE(e){\displaystyle l=4a\int \limits _{0}^{\pi /2}{\sqrt {1-e^{2}\cos ^{2}t}}\,dt=4aE(e)},

где E(e){\displaystyle E\left(e\right)} — .

Приближённые формулы для периметра

L≈4πab+(a−b)2a+b.{\displaystyle L\approx 4{\frac {\pi ab+(a-b)^{2}}{a+b}}.}

Максимальная погрешность этой формулы ~0,63 % при эксцентриситете эллипса ~0,988 (соотношение осей ~1/6,5). Погрешность всегда положительная.

Приблизительно в два раза меньшие погрешности в широком диапазоне эксцентриситетов дает формула:

L≈4⋅(ax+bx)(1x){\displaystyle L\approx 4\cdot \left(a^{x}+b^{x}\right)^{\left(1/x\right)}}, где x=ln⁡2ln⁡π2.{\displaystyle x={\frac {\ln 2}{\ln {\frac {\pi }{2}}}}.}

Максимальная погрешность этой формулы ~0,36 % при эксцентриситете эллипса ~0,980 (соотношение осей ~1/5). Погрешность также всегда положительная.

Существенно лучшую точность при ,05ab20{\displaystyle 0,05
обеспечивает формула Рамануджана:

L≈π3(a+b)−(3a+b)(a+3b).{\displaystyle L\approx \pi \left.}

При эксцентриситете эллипса ~0,980 (соотношение осей ~1/5) погрешность составляет ~0,02 %. Погрешность всегда отрицательная.

Ещё точней оказалась вторая формула Рамануджана:

L≈π(a+b)1+3(a−ba+b)210+4−3(a−ba+b)2{\displaystyle L\approx \pi (a+b)\left}

Точные формулы для периметра

Джеймс Айвори и Фридрих Бессель независимо друг от друга получили формулу для периметра эллипса:

L=π(a+b)1+∑n=1∞(2n−1)!!(2n−1)⋅2n⋅n!(a−ba+b)n2{\displaystyle L=\pi (a+b)\left^{2}\right]}

Альтернативная формула

L=2πaN(1−e2)M(1−e2),{\displaystyle L={\frac {2\pi aN(1-e^{2})}{M({\sqrt {1-e^{2}}})}},}

где M(x){\displaystyle M(x)} — Арифметико-геометрическое среднее 1 и x{\displaystyle x},
а N(x){\displaystyle N(x)} — 1 и x{\displaystyle x}, которое было введено С. Ф. Адлаем в статье 2012 года.

Список источников

• dict.sernam.ru
• geometry-and-art.ru
• wiki.sc
• howlingpixel.com
• www.astronet.ru
• topography.ltsu.org
• geo.web.ru

МЕТОДЫ ОПРЕДЕЛЕНИЯ ФИГУРЫ И РАЗМЕРОВ ЗЕМЛИ

При определении фигуры и размеров Земли использовались следующие методы:

Астрономо — геодезический метод

Определение фигуры и размеров Земли основано на использовании градусных измерений, суть которых сводится к определению линейной величины одного градуса дуги меридиана и параллели на разных широтах. Однако непосредственные линейные измерения значительной протяженности на земной поверхности затруднены, ее неровности существенно снижают точность работ.Метод триангуляции. Высокая точность измерения значительных по протяженности расстояний обеспечивается применением метода триангуляции, разработанного в XVII в. голландским ученым В. Снеллиусом (1580 – 1626).
Триангуляционные работы для определения дуг меридианов и параллелей проводились учеными разных стран. Еще в XVIII в. было установлено, что один градус дуги меридиана у полюса длиннее, чем у экватора. Такие параметры характерны для эллипсоида, сжатого у полюсов. Этим подтверждалась гипотеза И. Ньютона о том, что Земля в соответствии с законами гидродинамики должна иметь форму эллипсоида вращения, сплюснутого у полюсов.

Геофизический (гравиметрический) метод

Он основан на измерении величин, характеризующих земное поле силы тяжести, и их распределении на поверхности Земли. Преимущество этого метода в том, что его можно применять на акваториях морей и океанов, т. е. там, где возможности астрономо-геодезического способа ограничены. Данные измерений потенциала силы тяжести, выполненные на поверхности планеты, позволяют вычислить сжатие Земли с большей точностью, чем астрономо-геодезическим методом.
Начало гравиметрическим наблюдениям было положено в 1743 г. французским ученым А. Клеро (1713 – 1765). Он предположил, что поверхность Земли имеет вид сфероида, т. е. фигуры, которую приняла бы Земля, находясь в состоянии гидростатического равновесия под влиянием только сил взаимного тяготения ее частиц и центробежной силы вращения около неизменной оси. А. Клеро предположил также, что тело Земли состоит из сфероидальных слоев с общим центром, плотность которых возрастает к центру.

Космический метод

Развитие космического метода и изучения Земли связано с освоением космического пространства, которое началось с момента запуска советского искусственного спутника Земли (ИСЗ) в октябре 1957 г. Перед геодезией были поставлены новые задачи, связанные с бурным развитием космонавтики. В их числе – наблюдение за ИСЗ на орбите и определение их пространственных координат в заданный момент времени. Выявленные отклонения реальных орбит ИСЗ от предвычисленных, вызванные неравномерным распределением масс в земной коре, позволяют уточнить представление о гравитационном поле Земли и в конечном результате о ее фигуре.

Вопросы и задания для самоконтроля

1. Для каких целей используются данные о форме и размерах Земли?
2. По каким признакам в древности определили, что Земля имеет шарообразную форму?
3. Какую фигуру называют геоидом?
4. Какую фигуру называют эллипсоидом?
5. Какую фигуру называют референц-эллипсоидом?
6. Каковы элементы и размеры эллипсоида Красовского?
7. Назовите основные линии и плоскости земного эллипсоида.
8. Какие методы используются для определения фигуры и размеров Земли?
9. Дайте краткую характеристику каждому методу.

• Далее
• Главная
• Предыдущая

2.5 Два предела сжатия для фигур равновесия

Коснемся сначала истории нашего вопроса. И.Ньютон (1643-1727) для объяснения
явления, которое заметили многое астрономы, отъезжающие в экспедиции для
наблюдений солнечного затмения в экваториальную зону, астрономические часы
маятникового типа отстают по сравнению с Парижской обсерваторией, где они
строго выверялись, на 2,5 минуты в сутки. Ньютон предположил, что виной тому
служит эллипсоидальная форма Земли и, естественно, ее суточное вращение.
Предполагая, что Земля — однородный эллипсоид вращения, он получил, что
сжатие земного эллипсоида должно быть равным 1,25 =1:230.

Современник Ньютона Гюйгенс (1629-1695) решает ту же задачу, но другим
путем. Он предположил, что силы притяжения направлены к центру, а эллипсоидальность
поверхности уровня возникает только за счет центробежной силы. Таким
образом, если Ньютон в качестве фигуры равновесия брал эллипсоид Маклорена,
то Гюйгенс — фигуру, которую мы назвали «планетой Роша». Он получил, что
сжатие равно 0.5 = 1:576. Результат, который значительно отличается
Ньютоновской оценки сжатия.

Вернемся к теории Клеро. Согласно его теории сжатие равновесной планеты
должно быть равно
. Первый предел сжатия получим, если примем Земли однородным
двухосным эллипсоидом, для которого
,

. Отсюда
.

Но
,
,

.
Следовательно
и, наконец,

(4.19)

Мы получили то же значение, что и Ньютон, правда с точностью до первой
степени сжатия.

Второй предел сжатия, мы получим, если будем считать все притягивающие массы
шаром, тогда и

(4.20)

Таким образом. реальное сжатие лежит между этими двумя пределами

Для иллюстрации сказанного приведем сжатия некоторых планет Солнечной
системы, а также их возможные предельные значения

Название планеты	сжатие
по Ньютону	по Гюйгенсу	реальное
Земля	1:230	1:576	1:297
Марс	1:174	1:434	1:192
Юпитер	1:9,4	1:23,5	1:15
Сатурн	1:5,1	1:12,8	1:10
Уран	1:10,6	1:26,6	1:14

Сравнивая значения сжатия, мы видим, что фигура планеты в значительно
степени зависит от ее внутреннего строения. Планеты Земля и Марс весьма
далеки от того строения, которое принял Гюйгенс: планета имеет компактное
твердое притягивающее тело, окруженное рыхлой оболочкой. По величине сжатия
можно судить о том, что к такой модели более подходят планеты гиганты.

Приведенные данные взяты из книги акад. А.А. Михайлова «Курс гравиметрии и
теории фигуры Земли», опубликованной в 1939 году. Современные данные могут
несколько отличаться от приведенных, хотя общая картина не изменится.

4.1 Потенциал тяжести| Оглавление |
4.3 Гравитационные аномалии и … >>

Публикации с ключевыми словами: гравиметрия — геофизика — солнечная система — сейсмологияПубликации со словами: гравиметрия — геофизика — солнечная система — сейсмология
См. также: Все публикации на ту же тему >>

Мнения читателей

Астрометрия
—Астрономические инструменты
—Астрономическое образование
—Астрофизика
—История астрономии
—Космонавтика, исследование космоса
—Любительская астрономия
—Планеты и Солнечная система
—Солнце

Эллипс

Плоские фигуры > Окружность

Окружность является частным случаем эллипса. Наряду с гиперболой и параболой, эллипс является коническим сечением и квадрикой.Эллипс также можно описать как пересечение плоскости и кругового цилиндра или как ортогональную проекцию окружности на плоскость.

Эллипс — греч. недостаток, изъян

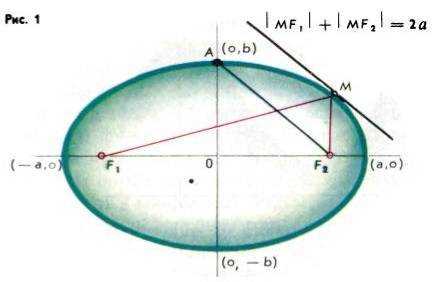Эллипс — одно из конических сечений. Его также можно определить как фигуру, состоящую из всех тех точек плоскости, сумма расстояний от которых до двух заданных точек F1 и F2 (называемых фокусами эллипса) является постоянной величиной, обычно обозначаемой через 2а .Из этого определения нетрудно установить, что прямая, проходящая через фокусы эллипса, есть его ось симметрии, как и прямая, являющаяся серединным перпендикуляром отрезка F1F2. Точка О пересечения этих прямых служит центром симметрии эллипса, его называют просто центром эллипса. Если взять указанные прямые в качестве осей координат, то уравнение эллипса запишется в виде х2/а2 + y2/b2 = 1.Из уравнения эллипса следует, что ось абсцисс эллипс пересекает в точках (а,О) и (-а,0), а ось ординат-в точках (b, ) и (—b, ). Эти четыре точки называются вершинами эллипса. Отрезок между вершинами на оси абсцисс называется большой осью, а на оси ординат- малой осью. Их отрезки от вершины до центра эллипса называются полуосями.Зная определение эллипса, можно сделать простейший прибор, вычерчивающий эллипс. Для этого надо связать две булавки ниткой и воткнуть их в чертежную доску, взять карандаш и двигать его по бумаге так, чтобы грифель карандаша все время натягивал нитку. Тогда кончик грифеля будет рисовать на бумаге эллипс.Второй способ построения эллипса основан на том факте, что при сжатии окружности к ее диаметру получается эллипс.  Отношение b/а характеризует «сплюснутость» эллипса. Чем меньше это отношение, тем сильнее вытянут эллипс вдоль большой оси. Однако степень вытянутости эллипса принято выражать через другой параметр, общий для всех конических сечений,-эксцентриситет Ɛ = с/а. Для разных эллипсов эксцентриситет меняется в пределах от 0 до 1, оставаясь всегда меньше единицы. У планет, которые, как известно, движутся по эллипсам, самый маленький эксцентриситет имеет орбита Венеры (0,0068), следующий по величине эксцентриситет у Нептуна (0,0086), затем у Земли (0,0167). Самый большой эксцентриситет у Плутона (0,253), однако он не идет ни в какое сравнение с эксцентриситетами комет. Так, комета Галлея имеет эксцентриситет 0,967.Тот факт, что эллипс является результатом сжатия окружности, объясняет, почему круглые предметы: колеса машин, иллюминаторы кораблей, циферблаты часов и т. д. — мы видим как эллипсы, если смотрим на них под углом.Одним из самых замечательных свойств эллипса является его оптическое свойство, состоящее в том, что прямые, соединяющие точку эллипса с фокусами, пересекают касательную к эллипсу в этой точке под разными углами. А это значит, что луч, пущенный из одного фокуса, после отражения попадет в другой. Это свойство лежит в основе интересного акустического эффекта, наблюдаемого в некоторых пещерах и искусственных сооружениях.Энциклопедическмй словарь юного математика, 1989

Главная | Геометрия и искусство | Плоские фигуры | Пространственные фигуры | Движения и преобразования | Орнаменты и стили | Доклад | Разное | Галерея | Главная Карта Сайта

Параметры земного эллипсоида

Земной эллипсоид имеет три основных параметра, любые два из которых однозначно определяют его фигуру:

• большая полуось (экваториальный радиус) эллипсоида, a;
• малая полуось (полярный радиус), b;
• геометрическое (полярное) сжатие, f=a−ba{\displaystyle f={\frac {a-b}{a}}}.

Существуют также и другие параметры эллипсоида:

• первый эксцентриситет, e=a2−b2a2=a2−b2a{\displaystyle e={\sqrt {\frac {a^{2}-b^{2}}{a^{2}}}}={\frac {\sqrt {a^{2}-b^{2}}}{a}}};
• второй эксцентриситет, e′=a2−b2b2=a2−b2b{\displaystyle e’={\sqrt {\frac {a^{2}-b^{2}}{b^{2}}}}={\frac {\sqrt {a^{2}-b^{2}}}{b}}}.

Для практической реализации земной эллипсоид необходимо ориентировать в теле Земли. При этом выдвигается общее условие: ориентирование должно быть выполнено таким образом, чтобы разности астрономических и геодезических координат были минимальными.

Основные формулы

2πa(a+b2a2−b2ln⁡(a+a2−b2b)){\displaystyle 2\pi a\left(a+{\frac {b^{2}}{\sqrt {a^{2}-b^{2}}}}\ln \left({\frac {a+{\sqrt {a^{2}-b^{2}}}}{b}}\right)\right)}, (для сплюснутого, a > b)

2πa(a+b2b2−a2arcsin⁡(b2−a2b)){\displaystyle 2\pi a\left(a+{\frac {b^{2}}{\sqrt {b^{2}-a^{2}}}}\arcsin \left({\frac {\sqrt {b^{2}-a^{2}}}{b}}\right)\right)}, (для вытянутого, a

Объём:

43πa2b{\displaystyle {\frac {4}{3}}\pi a^{2}b}

Здесь oε{\displaystyle o\!\varepsilon } — угловой эксцентриситет:

oε=arccos⁡(ba)=2arctan⁡(a−ba+b){\displaystyle o\!\varepsilon =\arccos \left({\frac {b}{a}}\right)=2\arctan \left({\sqrt {\frac {a-b}{a+b}}}\right)\quad \mathrm {} }, (сплюснутый)

=arccos⁡(ab)=2arctan⁡(b−ab+a){\displaystyle =\arccos \left({\frac {a}{b}}\right)=2\arctan \left({\sqrt {\frac {b-a}{b+a}}}\right)\quad \mathrm {} }, (вытянутый)

(sin(oε) часто выражается как , «e»)

2.3 Модель планеты Роша

Под «планетой Роша» мы будем понимать такую фигуру равновесия, в которой
вся притягивающая масса сосредоточена в и одной точке — центре масс, а
вектор силы тяжести образуют векторная сумма силы притяжения и центробежной
силы. Тогда уравнением «поверхности» такой планеты будет

(4.8)

Рассмотрим, сначала, как выглядит поверхность уровня вблизи начала
координат. В этом случае величину
можно
считать малой, а , наоборот, большой. Пренебрегая в () вторым
слагаемым в левой части формулы, получим
. Это
уравнение замкнутой поверхности, которая по мере приближения к началу
координат становится все более похожей на сферу. Назовем ее псевдосферой.

По мере отдаления от начала координат в плоскости мы достигнем таких
точек, в которых сила притяжения и центробежная сила становятся равными и
противоположно направленными, то есть
,
Отсюда
. Мы получили уравнение окружности с
радиусом, равным
Понятно, что во всех
точках этой окружности силы тяжести равна нулю.

Если двигаться дальше от начала координат, мы придем к варианту, когда

будет большой величиной, а , наоборот, малой. Тогда
пренебрегая первым членом в формуле (), получим уравнение поверхности,
близкой к круговому цилиндру
.
Это уже разомкнутая поверхность уровня. Планеты с такой поверхностью
существовать не может.

Таким образом, гидростатически равновесная планета может существовать только
внутри «полости Роша», где сила тяжести всюду отлична от нуля и направлена
по нормали внутрь этой поверхности. Поверхность такой планеты имеет овальную
форму, сплюснутую с полюсов.