Что такое земной сфероид простыми словами

6.1 Нормальный потенциал тяжести

Общепризнанно, что наиболее удобным геометрическим телом для модели Земли
является общеземной эллипсоид (ОЗЭ) — уровенный эллипсоид вращения. Его
гравитационный потенциал (потенциал тяжести!)
называют
нормальным потенциалам. Условие для выбора параметров нормальной Земли:

1. Центр масс и ось вращения нормальной Земли совпадают соответственно с
   центром масс и осью вращения реальной Земли.

2. Угловая скорость вращения эллипсоида и реальной Земли совпадают.

3. Масса эллипсоида равна массе Земли.

4. Зональный коэффициент разложения потенциала второй степени реальной Земли
   равен соответствующему коэффициенту нормальной Земли.

Обозначения параметров нормальной Земли мы будем отмечать верхним или нижним
индексом «0».

Итак, потенциал тяжести реальной Земли имеет вид

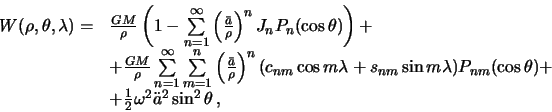(6.1)

где — средний экваториальный радиус Земли. Учитывая, что потенциал
эллипсоида вращения содержит только зональные гармоники можно записать

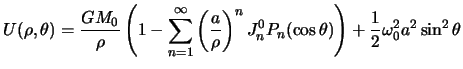(6.2)

Условие для выбора параметров нормальной Земли:

Эти четыре параметра подлежат уточнению, по мере накопления новых данных.
Астрономо-геодезические исследования нуждаются в единой системе
фундаментальных постоянных. Такая система обычно устанавливается на крупных
международных собраниях ученых. На Генеральной Ассамблее Международного
Астрономического Союза (МАС) в 1976 г принято

Несколько позже мы докажем замечательную теорему Стокса, которая утверждает,
что, если известна поверхность планеты, являющаяся поверхностью уровня,
которая охватывает все массы, известна также планетоцентрическая
гравитационная постоянная и угловая скорость вращения , то
гравитационное поле может быть однозначно определено во внешнем
пространстве. Число параметров, определяющих эллипсоид вращения равно двум
(большая и малая полуоси). Следовательно всего нам нужно знать четыре
параметра, остальные определяются через геоцентрическую гравитационную
постоянную, угловую скорость вращения, большую полуось и сжатие планеты. В
формулу () входят бесчисленное множество параметров. Однако теория
показывает, все стоксовы постоянные определяются через уже упомянутые четыре
параметра.

Поскольку последовательность
для гидростатически
равновесных фигур убывает достаточно быстро, часто в формуле () для
нормального потенциала ограничиваются только первым членом суммы. Тогда
нормальный потенциал тяжести принимает вид

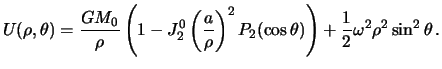(6.3)

Отбрасывание малых членов в разложении потенциала приводит к тому, что
поверхность
где — постоянная величина,
уже перестает, строго говоря, быть эллипсоидом. Такую поверхность, близкую к
сфере, называют сфероидом.

Перепишем уравнение сфероида в следующем виде

(6.4)

Введем обозначение
.
Формула ()
теперь принимает вид

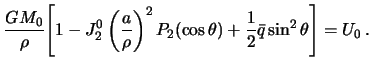
Поскольку и —
малые величины, уравнение сфероида можно представить так

(6.5)

следовательно,

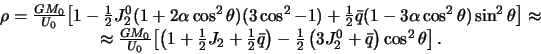
Сравнивая полученное выражение с (), получим

(6.6)

Таким образом, сжатие равновесной планеты зависит от стоксовой постоянной

и безразмерной угловой скорости вращения

, которая имеет простой физический
смысл: это отношение центробежной силы на экваторе к величине, достаточно
близкой к силе тяжести на экваторе. Такой гидростатически равновесный
сфероид носит название сфероида Клеро, по имени французского математика, работавшего над
теорией равновесных фигур планет.

Сжатие для сфероида Клеро можно записать и так

При выводе формулы для сжатия планеты мы не пользовались никакими гипотезами
о ее строении. Клеро же рассматривал гидростатически равновесную модель,
полагая, что массы распределены в виде тонких сфероидальных слоев. Им
построена не только зависимость сжатия планеты от ее угловой скорости
вращения, но и сжатии внутренних слоев. Показано, что эти сжатия уменьшаются
по мере приближения к центру планеты.

Остается определить закон изменения силы тяжести с широтой на сфероиде Клеро
также с точностью до сжатия. Из формулы () следует

Сила тяжести на экваторе

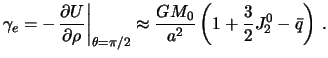
Сила тяжести на полюсе

Отношение

иногда называют гравитационное сжатие.
Из приведенных выше формул следует

Геодезия

Геоид

Для правильного изучения размеров и формы Земли используется геодезия, отрасль науки, ответственная за измерение размера и формы Земли с помощью обследований и математических расчетов.

На протяжении всей истории, геодезия была важной отраслью науки, так как ранние ученые и философы пытались определить форму Земли. Аристотель — первый человек, которому приписывают попытку рассчитать размер Земли и, следовательно, ранний геодезист

Затем последовал греческий философ Эратосфен, оценивший окружность Земли в 40 233 км, что лишь немного больше принятого в наши дни измерения.

Чтобы исследовать Землю и использовать геодезию, исследователи часто ссылаются на эллипсоид, геоид и референц-эллипсоид. Эллипсоид является теоретической математической моделью, которая показывает гладкое, упрощенное представление о поверхности Земли. Он используется для измерения расстояний на поверхности без учета таких факторов, как изменения высоты и формы рельефа

С учетом реальности земной поверхности, геодезисты используют геоид — модель планеты, которая строится с помощью глобального среднего уровня моря и, следовательно, принимает во внимание перепады высот

Основой геодезии на сегодняшний день являются данные, которые выступают в качестве ориентиров для глобальных геодезических работ. Сегодня такие технологии, как спутники и глобальные системы позиционирования (GPS), позволяют геодезистам и другим ученым делать чрезвычайно точные измерения поверхности Земли. На самом деле они настолько точны, что позволяют получать данные о поверхности Земли с точностью до сантиметров, обеспечивая наиболее точные измерения размера и формы Земли.

Мне нравится26Не нравится6

Определение различных сфероидов для точного картографирования

Чтобы помочь нам лучше понять объекты земной поверхности и особенности ее неровностей, неоднократно проводились геодезические съемки Земли. Эти исследования дали определение многих сфероидов, описывающих форму Земли. Как правило, сфероид выбирается для одной страны или определенной территории. Сфероид, наилучшим образом подходящий для одного географического региона, не обязательно подойдет для другого региона. До недавнего времени в геодезических измерениях в Северной Америке использовался сфероид, определенный Кларком в 1866. Большая полуось сфероида Кларка 1866 равна 6,378,206.4 метра, а малая полуось — 6,356,583.8 метра.

Из-за гравитационных различий и разнообразия объектов поверхности, Земля не является ни правильной сферой, ни правильным сфероидом. Использование спутниковых технологий позволило выявить несколько отклонений от правильного эллипса; например, Южный полюс расположен ближе к экватору, чем Северный полюс. Сфероиды, определенные при помощи спутников, вытесняют старые сфероиды, полученные с использованием наземных вычислений. Например, новым стандартом сфероида для Северной Америки является “Геодезическая система привязки 1980 года” (Geodetic Reference System of 1980 – GRS 1980), радиусы которого равны 6378137,0 и 6356752,31414 метрам. Параметры сфероида GRS 1980 были утверждены Международным Союзом геодезистов и геофизиков в 1979 г.

6.4 ѓравитационный потенциал эллипсоида вращениЯ

ђассмотрим случай, когда уровеннаЯ поверхность есть эллипсоид вращениЯ.
“равнение этой поверхности в декартовых координатах имеет вид

Џерейдем к гиперболической системе координат
(см. лекцию 2, раздел )

Љак мы видели, уравнение эллипсоида вращениЯ с полуосЯми

,

имеет вид . „лЯ определениЯ
потенциала притЯжениЯ на поверхности уровенного эллипсоида

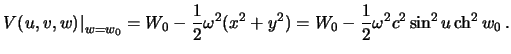
€так, нам известен потенциал притЯжениЯ на поверхности эллипсоида. ’ребуетсЯ
определить его во всем внешнем пространстве. Џоскольку потенциал притЯжениЯ
— гармоническаЯ функциЯ, она подчинЯетсЯ дифференциальному уравнению
‹апласа, которое можно написать в виде

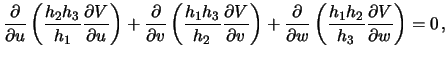
где
—
коэффициенты ‹аме. Ћпределим их

(6.8)

‚ычислим отношениЯ коэффициентов ‹аме, стоЯщие в дифференциальном уравнении
‹апласа

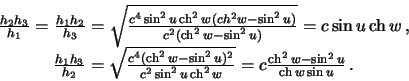(6.9)

€так, уравнение ‹апласа длЯ функции принимает вид

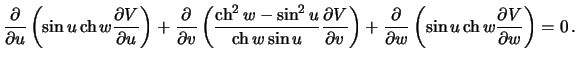(6.10)

Џолученное дифференциальное уравнение линейно, поэтому будем искать решение
в виде суммы гармонических функций. ‚ силу осевой симметрии эллипсоида
вращениЯ и того, что граничные условиЯ не зависЯт от переменной — аналога
долготы, то и решение уравнениЯ не должно содержать этой переменной. €ными
словами ищем решение в виде

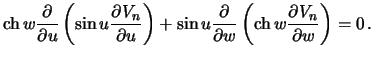(6.11)

Љак и в случае решениЯ дифференциального уравнениЯ длЯ сферических функций,
будем искать решение в виде произведениЯ двух функций, каждаЯ из которых
ЯвлЯетсЯ функцией одной переменной

(6.12)

Џодставим решение, заданное в виде () в уравнение ()
и поделим
полученное уравнение на
:

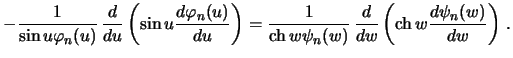
Џолученное уравнение справедливо при любых значениЯх независимых переменных.
ќто возможно лишь в том случае, когда обе части этого уравнениЯ равны одной
и той же постоЯнной. Ћбозначим эту постоЯнную через . Џолучим два
дифференциальных уравнениЯ

(6.13)

Џокажем, что первое из приведенных здесь уравнений при
есть уравнение длЯ
полиномов ‹ежандра (см. лекцию 3, уравнениЯ ()-()),
то есть

(6.14)

Џоложим
,
, тогда вместо первого
из уравнений () будем иметь

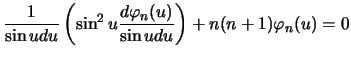
или

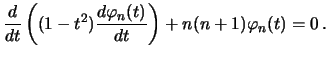(6.15)

“равнение () совпадает с уравнением длЯ полиномов ‹ежандра
(см. лекцию 3, формула ())

€так, решением уравнениЯ ‹апласа в гиперболической системе координат будет
функциЯ

(6.16)

котораЯ на поверхности эллипсоида принимает значениЯ

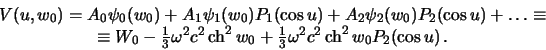(6.17)

Џри выводе формулы () мы принЯли во внимание, что

. ‘равниваЯ левую и правую части
формулы () мы приходим к выводу, что

(6.18)

€так, в формуле () длЯ потенциала притЯжениЯ
эллипсоида отличные от нулЯ
только коэффициенты и , поэтому строгое
выражение длЯ потенциала в гиперболических координатах
можно записать в виде

(6.19)

ЋстаетсЯ определить функции
и
. Љак следует
из уравнений (), функцию
можно определить,
решив второе
из названных уравнений при и при   
:

(6.20)

Џолученным дифференциальным уравнениЯм удовлетворЯют функции

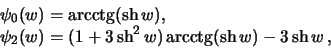
в чем можно убедитсЯ простой подстановкой в уравнениЯ ().

€збавимсЯ теперь от гиперболических функций, полученных нами при решении
дифференциальных уравнений. Љак мы уже говорили, переменнаЯ определЯет
семейство софокусных эллипсоидов. ‚озьмем некоторую точку на оси вращениЯ
эллипсоида, находЯщуюсЯ на расстоЯнии от центра. ’огда длЯ этой точки
,
.
‡аменим переменную на
:

(6.21)

€так, потенциал притЯжениЯ в произвольной точке вне эллипсоида имеет вид

(6.22)

Љоэффициенты и определим из краевого условиЯ

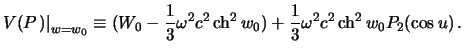
‡аметим, что
,
, после соответствующих преобразований
получим

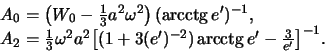(6.23)

”ормулы () и () определЯют потенциал притЯжениЯ эллипсоидальным
телом материальной точки, лежащей на поверхности софокусного эллипсоида

‡наЯ координаты точки и полуоси эллипсоида и легко определить
параметр , а следовательно и малую полуось

эллипсоида, проходЯщего через заданную точку.

€з приведенных формул видно, что потенциал притЯжениЯ содержит лишь четыре
независимых параметра
и .
ќти четыре параметра абсолютно строго
определЯют потенциал притЯжениЯ эллипсоидальным телом материальной точки,
лежащей во вешнем пространстве, при любом распределении масс внутри тела
лишь бы его поверхность оставалась поверхностью уровнЯ.

Лекция 6. Нормальная Земля

Нормальный потенциал тяжести. Четыре фундаментальных постоянных,
определяющих потенциал тяжести. Сфероид Клеро. Теорема Стокса.
Гравитационный потенциал эллипсоида вращения. Дифференциальные
уравнения, определяющие потенциал притяжения эллипсоида.
Условия гидростатического равновесия эллипсоида вращения.

Термин нормальная Земля — традиционный среди специалистов-геодезистов. Слово нормальная применительно
к силе тяжести, высоте и т.п. означает, что данный параметр является
предсказуемым. Его можно вычислить по известным формулам. Нормальная Земля —
это тело отсчета для построения карт высот, глубин морей и т.д. Причем, это
тело должно описываться достаточно простыми математическими формулами и,
кроме того, достаточно хорошо аппроксимировать физическую поверхность
планеты.

Форма и размеры Земли

Традиционно принято считать, что Земля имеет форму шара. Однако это не совсем так.

Первые исследователи считали, что Земля плоская и представляет собой диск, плавающий на поверхности воды. Их взгляды кардинально изменил Аристотель, который не просто предположил, что наша планета круглая, но и доказал это. Сегодня для простоты Землю также называют шаром. Однако не секрет, что из-за вращения вокруг своей оси и возникающей при этом центробежной силы наша планета не может иметь абсолютно шарообразную форму.

Параметры Земли

• Масса — 5,97 х 1024 кг.
• Объем — 108,3 х 1010 км3.
• Длина экватора — 40 075,7 км.
• Длина меридиана — 40 008,5 км.
• Экваториальный радиус — 6378,2 км.
• Полярный радиус — 6356,8 км.

Соотношение размеров Солнца, Земли и других планет Солнечной системы

Земля — эллипсоид?

Первоначально предполагалось, что Земля имеет форму эллипсоида — она несимметрична и сплюснута у полюсов. Подтверждением этому служит тот факт, что экваториальный радиус на 21,4 км больше, чем расстояние от центра Земли до полюсов (полярный радиус). Кроме того, более точные измерения показали, что расстояние от экватора до Северного полюса меньше, чем до Южного.

Наглядная разница между шаром и эллипсоидом

А может, все-таки геоид?

Эллипсоид (как и шар) — идеальная форма, которую в действительности Земля не может иметь. Данная форма удобна для проведения математических расчетов, поэтому часто используется. Реальная же форма Земли далека от эталона. Она определяется неровностями рельефа материков и океанического дна, такими как впадины и возвышенности, и называется геоидом (что в переводе с греческого языка означает «землеподобный»).

Модель Земли

Сравнение поверхностей. Геоид — форма Земли, полученная мысленным продолжением поверхности Мирового океана под континентами

Определение сфероида

Основой сферы является круг, в то время как сфероид (или эллипсоид) основан на эллипсе.

Сфероид или эллипсоид — это тело, образованное вращением эллипса вокруг малой оси.

Форма эллипса определяется двумя радиусами. Более длинный радиус называется большой полуосью, а меньший (короткий) — малой полуосью.

Большая полуось или экваториальный радиус — это половина большой оси, а малая полуось или полярный радиус — половина малой оси.

Вращение эллипса вокруг малой оси образует эллипсоид. Сплющенный у полюсов эллипсоид вращения также известен как сфероид На рисунке показаны большая и малая оси сфероида.

Большая полуось находится в плоскости экватора, малая полуось ей перпендикулярна.

Сфероид определяется либо большой полуосью a и малой полуосью b, либо величиной a и сжатием. Сжатие — отношение разности длин между двумя осями к длине большой полуоси, выраженное простой или десятичной дробью. Сжатие, f, рассчитывается следующим образом:

Сжатие выражается маленькой величиной, поэтому обычно вместо него используется величина 1/f. Ниже представлены параметры World Geodetic System of 1984 (WGS 1984 или WGS84):

Сжатие варьируется от 0 до 1.Значение 0 значит, что оси равны, таким образом, эллипсоид является сферой. Сжатие Земли приблизительно равно 0,003353. Другим показателем, который подобно сжатию описывает форму сфероида, является квадрат эксцентриситета, e2. Он выражается следующей формулой:

Первые упоминания о геометрии Земли

С древних времен люди задумывались о форме нашей планеты и пытались объяснить ее геометрию.

Зародыш геометрического понимания Земли можно встретить у греков. Они считали Землю плоской и окруженной океаном. Однако уже Пифагор, живший в VI веке до нашей эры, выдвинул гипотезу о сферической форме Земли.

Первым, кто дал объективное доказательство сферичности Земли, стал греческий математик и астроном Эратосфен. В III веке до нашей эры он вычислил окружность Земли, измеряя угол между зенитом (прямой линией от точки наблюдения на поверхности Земли до ее центра) в разных точках на поверхности планеты. В его расчетах была допущена погрешность всего 2%, что для того времени можно считать невероятным достижением.

В Средние века теория сферичности Земли была забыта, но в эпоху Возрождения, благодаря работам ученых таких как Коперник и Галилео Галилей, она была восстановлена и утверждена научным сообществом как достоверное знание.

Свершившееся впоследствии открытие Америки Колумбом также свидетельствует о сферичности Земли. Если бы Земля была плоской, то мореплаватели не могли бы пройти с запада на восток через Атлантический океан, потому что Средиземноморское море не соединено с Тихим океаном.

6.3 ’еорема ‘токса

ќта теорема доказывает единственность внешней краевой задачи теории
потенциала. „ругими словами, если некоторое тело равномерно вращаетсЯ с
известной угловой скоростью, его поверхность, ЯвлЯющаЯсЯ поверхностью
уровнЯ, котораЯ охватывает всю массу, также известна, то потенциал тЯжести и
его первые производные будут однозначно определены как на поверхности ,
так и во всем внешнем пространстве.

’еорема доказываетсЯ от противного. Џредположим, что существует два
различных потенциала тЯжести и ,
которые принимают на поверхности постоЯнные значениЯ
и . ’аким образом,
,

,
где черта сверху означает, что значениЯ функции
относЯтсЯ к поверхности . Џоскольку потенциал
тЯжести есть сумма потенциала
тЯготениЯ и центробежного потенциала, то

Ћбозначим разность
. ЏолученнаЯ
функциЯ гармоническаЯ, так как потенциал притЯжениЯ — гармоническаЯ
функциЯ, удовлетворЯющаЯ во внешнем пространстве уравнению ‹апласа.

Џрименим первую формулу ѓрина (см. лекцию 3, раздел ???)
длЯ случаЯ, когда и . ‚ыберем, в
качестве «тела» по которому нужно выполнить интегрирование —
пространство, лежащее между поверхностью и сферой с очень большим
радиусом, так чтобы наша поверхность была целиком внутри сферы. Ћбозначим
это пространство через . ’еперь перваЯ формула ѓрина будет выглЯдеть
следующим образом

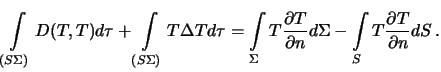(6.7)

‡нак минус между интегралами в правой части полученной формулы означает лишь
то, что внешнЯЯ нормаль длЯ одной поверхности ЯвлЯетсЯ внутренней длЯ другой
поверхности. ђассмотрим последний интеграл. ”ункциЯ
на поверхности —
постоЯннаЯ величина, равнаЯ
, поэтому

’

ђассмотрим теперь второй интеграл в правой части выражениЯ ().
ЏроизводнаЯ по нормали к сфере есть производнаЯ по радиус-вектору. Џоскольку
длЯ очень большого радиуса исходное тело можно считать материальной точкой,
то
. Ђналогично
,
где — постоЯннаЯ величина. Ћтсюда следует

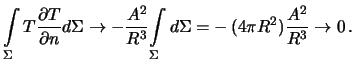
‚ левой части равенства () нужно положить
, так как
— функциЯ гармоническаЯ, поэтому это выражение принимает вид

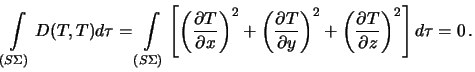
Џоскольку подынтегральное выражение не может быть отрицательным ни при каких
значениЯх координат, остаетсЯ сделать вывод, что — постоЯннаЯ величина во
всем внешнем пространстве. Ќо на сфере с бесконечно большим радиусом она
равна нулю и в силу непрерывности она равна нулю и на поверхности . ’аким
образом T(x,y,z)=0 во всем внешнем пространстве, то есть

, что и доказывает теорему.

Земной Сфероид своими словами для детей

Земной сфероид — это форма, которую приняла бы Земля, если бы она была сделана из воды и находилась в состоянии равновесия под влиянием только сил притяжения между разными частями Земли.

Земля — это большой шар, на котором мы живем. Но на самом деле, Земля немного несовершенна и имеет несколько неровностей. Если мы представим, что Земля сделана из воды и все неровности стали бы ровными, то она приняла бы форму, которую называют земным сфероидом.

Эта форма похожа на шар, но немного вытянута в полюсах и сплюснута на экваторе. То есть, если мы представим, что Земля — это огромный мяч, то он был бы немного подобен футбольному мячу, который не совсем круглый.

Почему это происходит? Все дело в силах притяжения между разными частями Земли. Эти силы притяжения вызывают неравномерное распределение массы Земли. Например, на экваторе Земли сила притяжения немного слабее, чем на полюсах. Из-за этого, материалы Земли распределены неравномерно, что и приводит к форме земного сфероида.

Таким образом, земной сфероид — это форма, которая была бы у Земли, если бы она была ровной и сделана из воды. Она немного вытянута в полюсах и сплюснута на экваторе из-за неравномерного распределения массы Земли под влиянием сил притяжения.

Форма Земли

Земля представляет собой приплюснутый сфероид – этот термин используют для описания формы планеты. У Земли есть два полярных диаметра – это линия, которая проходит через северный и южный полюс. Диаметр, проходящий через экватор – это экваториальный диаметр. В сравнении с полярными диаметрами, экваториальный диаметр больше на 21 км.

Причиной приплюснутости Земли с полюсов является ее вращение вокруг своей оси. Концентрация массы вблизи экватора и ее отсутствие у полюсов, когда Земля вращается вокруг своей оси, вызывает центробежную силу. Эта сила влияет на плотность материи, вращающейся вместе с планетой, и приводит к приплюснутой форме.

Форма Земли может изменяться в зависимости от различных факторов, таких как силы гравитации, движение магмы, тектонические процессы и изменения климата. Однако, эти изменения очень медленные, и форма Земли почти не меняется за годы, даже за века.

• Многие другие планеты в нашей Солнечной системе также имеют приплюснутую форму, но в них этот эффект не так ярко выражен, как на Земле.
• Существует различие между геоцентрической формой Земли — когда она рассматривается в качестве твердого тела — и геодезической формой — когда ее рассматривают как форму поверхности.

Итак, форма Земли является результатом вращения планеты вокруг своей оси и составляет приплюснутый сфероид.

Движение Земли

Сквозь бескрайние просторы Вселенной, среди бесчисленного множества звезд мчится планета, которую мы называем своим домом, — Земля. Нам она кажется необъятным миром, но это лишь иллюзия. В суматохе дней мы редко всматриваемся в небо и не осознаем, что в необозримой пустоте космоса наша планета не более чем песчинка, на которой возникло чудо жизни.

Земля — космическое тело, а мы — космонавты, совершающие длительный полет вокруг Солнца и бороздящие, не думая о том, просторы Вселенной. На протяжении веков люди пытались выяснить, что из себя представляет этот «космический корабль», пассажирами которого они стали. Какой он формы, с какой скоростью мчится? Благодаря человеческому любопытству, упорству исследователей, а затем и научно-техническому прогрессу сегодня почти на все вопросы о Земле у нас есть точные ответы.

Земля, как и другие планеты солнечной системы, находится в постоянном движении. Движение — это жизнь. Данное утверждение справедливо не только для человека, но и для нашей планеты. Каждую секунду мы перемещаемся в космическом пространстве со скоростью около 30 км/с, совершая не одно, а несколько типов движения.

Два основных типа движения Земли и их следствия: а) осевое вращение; б) орбитальное вращение.

Осевое вращение

Первое и наиболее ощутимое для нас — движение Земли вокруг своей оси. День сменяет ночь, а ночь сменяет день, обеспечивая бесконечное течение времени. Наверное, каждый человек хотя бы раз в жизни хотел, чтобы в сутках было больше чем 24 ч, ведь их не всегда хватает на запланированные дела. Оказывается, времени и того меньше! Полный оборот вокруг своей оси Земля совершает за 23 ч 56 мин 4,1 с.

Земля вращается вокруг своей оси с запада на восток

Движение Земли вокруг своей оси во многом напоминает запущенный волчок, ось которого при постепенном замедлении начинает описывать в пространстве конусы. Перемещаясь в космическом пространстве, подобные действия совершает и земная ось, что с течением времени неизбежно приводит к изменению координат светил на звездном небе. Полный цикл земной прецессии составляет около 25 800 лет.

Орбитальное вращение

Второй тип движения — вращение вокруг Солнца. Его наша планета совершает не по строго круговой орбите, а по слегка вытянутой в форме эллипса. Самая близкая к нашему светилу точка земного пути называется перигелием, а самая дальняя — афелием. В афелии мы находимся в июле, а в перигелии — в январе. Земля парит в пространстве не строго перпендикулярно своей орбите, а под наклоном, равным 23,5°. Наклон земной оси и орбитальное вращение обеспечивают неравномерный нагрев поверхности планеты в течение года, из-за чего происходит смена времен года.

Если рассматривать движения Земли в космических масштабах, то можно заметить, что в этих периодах нет круглых чисел, к которым мы привыкли. Например, звездный год — точное время оборота Земли вокруг Солнца — составляет 365 сут. и 6 ч. Лишние шесть часов мы отбрасываем в течение трех лет. Впоследствии они накапливаются и добавляются к каждому четвертому году, который называется високосным.

Схема движения Земли вокруг Солнца